ЕГЭ профиль № 13
Цилиндр + угол между прямыми

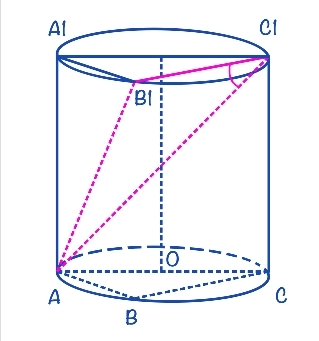
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А, В и С, а на окружности другого основания - точка С1, причём СС1 - образующая цилиндра, а АС - диаметр основания. Известно, что ∠АСВ = 30°, АВ = √2, СС1 = 4.

а) Докажите, что угол между прямыми АС1 и ВС равен 60°

б) Найдите площадь боковой поверхности цилиндра

Решение:












a) Проведём B1C1 параллельно ВС, тогда ∠(АС1;ВС) = ∠(AC1;B1C1) = ∠AC1B1

△ABC - прямоугольный, так как АС - диаметр окружности

△АВС: sin∠ACB = AB/AC → 1/2 = √2/AC → AC = 2√2 → AO = CO = r = √2

cos∠ACB = BC/AC → √3/2 = BC/(2√2) → BC = √6 = B1C1

△ACC1: AC1² = AC²+CC1² = 8+16 = 24 → AC1 = 2√6

△AA1B1: AB1² = AA1²+A1B1² = 16+2 = 18→ AB1 = 3√2

△AB1C1: AB1² = AC1²+B1C1²-2AC1B1C1cos∠AC1B1

18 = 24+6-22√6√6cos∠AC1B1

cos∠AC1B1 = 1/2 → ∠AC1B1 = ∠(АС1;ВС) = 60°

б) Пусть площадь боковой поверхности = S

S = 2πrh, где r - радиус окружности, h - высота цилиндра

S = 2π√24 = 8√2π = 8√2π

Ответ: б) 8√2π